[분할과 정복] 울타리 잘라내기(문제 ID:FENCE, 난이도:중) 본문
반응형
1. 문제정의
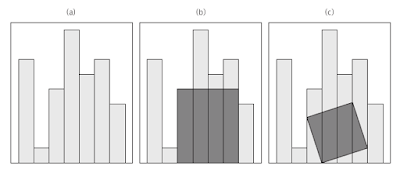
너비가 같은 N개의 나무 판자를 붙여 세운 울타리가 있습니다. 시간이 지남에 따라 판자들이 부러지거나 망가져 높이가 다 달라진 관계로 울타리를 통째로 교체하기로 했습니다. 이 때 버리는 울타리의 일부를 직사각형으로 잘라내 재활용하고 싶습니다. 그림 (b)는 (a)의 울타리에서 잘라낼 수 있는 많은 직사각형 중 가장 넓은 직사각형을 보여줍니다. 울타리를 구성하는 각 판자의 높이가 주어질 때, 잘라낼 수 있는 직사각형의 최대 크기를 계산하는 프로그램을 작성하세요. 단 (c)처럼 직사각형을 비스듬히 잘라낼 수는 없습니다.
판자의 너비는 모두 1이라고 가정합니다.
입력
첫 줄에 테스트 케이스의 개수 C (C≤50)가 주어집니다. 각 테스트 케이스의 첫 줄에는 판자의 수 N (1≤N≤20000)이 주어집니다. 그 다음 줄에는 N개의 정수로 왼쪽부터 각 판자의 높이가 순서대로 주어집니다. 높이는 모두 10,000 이하의 음이 아닌 정수입니다.
출력
각 테스트 케이스당 정수 하나를 한 줄에 출력합니다. 이 정수는 주어진 울타리에서 잘라낼 수 있는 최대 직사각형의 크기를 나타내야 합니다.
2. 문제 설계
분할과 정복 알고리즘을 설계하기 위해서는 부분문제로 어떻게 나눌지 결정해야한다. n개 판자를 절반으로 나눠 두 개의 부분 문제를 만들면, 우리가 찾는 최대 직사각형은 세 가지 중 하나일 것이다.
- 가장 큰 사각형은 '왼쪽' 부분 문제에서만으로 결정된다.
- 가장 큰 사각형은 '오른쪽' 부분 문제에서만으로 결정된다.
- 가장 큰 사각형은 '양쪽' 부분 문제 걸쳐서 결정된다.
부분 문제 정의판자를 반으로 나누어 왼쪽에서만 찾을 것인지, 오른쪽에서만 찾을 것인지, 양쪽에서 찾을 것인지 결정한다.
3. 구현
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int solve(vector<int> &fence, int left, int right){
//기저 사례:판자가 하나밖에 없는 경우
if (left == right)
return fence[left];
//반으로 나눠 두 구간으로 문제 분할
int mid = (left + right) / 2;
//분할한 문제를 각개격파
int ret = max(solve(fence, left, mid), solve(fence, mid+1, right));
//부분 문제 3:두 부분에 모두 걸치는 사각형 중 가장 큰 것
int low = mid; //왼쪽 끝
int high = mid + 1; //오른쪽 시작
int height = min(fence[low], fence[high]);
//[mid, mid+1]만 포함하는 너비 2인 사각형 고려
ret = max(ret, height * 2);
//사각형이 입력 전체를 덮을 때까지 확장
while (left < low || high < right){
//항상 높이가 더 높은쪽으로 확장
if (high<right && (low==left || fence[low-1]<fence[high+1])){
high++;
height = min(height, fence[high]);
}
else{
low--;
height = min(height, fence[low]);
}
//확장 후 사각형의 넓이
ret = max(ret, height*(high - low + 1));
}
return ret;
}
int main(void){
int testCase, num;
cin >> testCase;
for (int i = 0; i < testCase; i++){
cin >> num;
vector<int> fence(num, 0);
for (int j = 0; j < num; j++
cin >> fence[j];
cout<<"OUTPUT : "<<solve(fence, 0, fence.size() - 1)<<endl;
}
return 0;
}4. 테스트

반응형
'알고리듬' 카테고리의 다른 글
| [트리] 트리(Tree) 순회 (0) | 2021.06.01 |
|---|---|
| [DP] LCS(Longest Common Subsequence) 알고리듬 (0) | 2021.05.25 |
| [분할과 정복] 쿼드 트리 뒤집기(문제 ID:QUADTREE, 난이도:하) (0) | 2021.05.24 |
| 알고리듬 분석 (0) | 2021.05.21 |
| 알고리듬 개요 (0) | 2021.05.21 |
Comments


