[트리] 트리(Tree) 순회 본문
반응형
1. 문제정의
전산학에서 트리 순회(Tree traversal)는 트리 구조에서 각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정을 말한다. 이는 노드를 방문하는 순서에 따라 분류된다. 여기서 설명하는 알고리즘은 이진 트리에 대해서 작성되었지만, 다른 모든 트리에서도 일반화될 수 있다.
2. 문제 설계
연결 리스트와 1차원 배열과 같은 선형 자료 구조에서는 한 가지의 논리적인 순회 방법만이 존재하지만, 트리 구조의 순회에는 많은 방법이 존재한다. 이진 트리의 루트 노드에서 시작해서, 세 가지 주요 단계를 거치며 순회를 진행하는데, 그 단계에는 현재 노드를 방문하는 것, 왼쪽 자식 노드를 순회하는 것과 오른쪽 자식 노드를 순회하는 것이 있다. 이러한 과정은 재귀로 쉽게 설명할 수 있다.
전위 순회
전위 순회(preorder)는 다음과 같은 방법으로 진행한다. 루트 노드에서 시작해서,
- 노드를 방문한다.
- 왼쪽 서브 트리를 전위 순회한다.
- 오른쪽 서브 트리를 전위 순회한다.
전위 순회는 깊이 우선 순회(depth-first traversal)라고도 한다.
중위 순회
중위 순회(Inorder)은 다음의 순서로 진행된다.
- 왼쪽 서브 트리를 중위 순회한다.
- 노드를 방문한다.
- 오른쪽 서브 트리를 중위 순회한다.
중위 순회는 대칭 순회(symmetric)라고도 한다.
후위 순회
후위 순회(postorder)는 다음과 같은 방법으로 진행한다.
- 왼쪽 서브 트리를 후위 순회한다.
- 오른쪽 서브 트리를 후위 순회한다.
- 노드를 방문한다.
레벨 순서 순회
레벨 순서 순회(level-order)는 모든 노드를 낮은 레벨부터 차례대로 순회한다. 레벨 순서 순회는 너비 우선 순회(breadth-first traversal)라고도 한다.
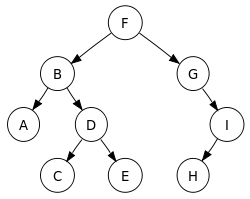
이진 탐색 트리에서
- 전위 순회: F, B, A, D, C, E, G, I, H (root, left, right)
- 중위 순회: A, B, C, D, E, F, G, H, I (left, root, right)
- 후위 순회: A, C, E, D, B, H, I, G, F (left, right, root)
- 레벨 순서 순회: F, B, G, A, D, I, C, E, H
3. 구현
#include <iostream>
#define null 0
using namespace std;
template <typename T>
class Tree;
template <typename T>
class TreeNode {
friend class Tree<T>;
private:
T data;
TreeNode* left;
TreeNode* right;
public:
TreeNode(T data = 0, TreeNode* left = null, TreeNode* right = null) {
this->data = data;
this->left = left;
this->right = right;
}
};
template <typename T>
class Tree {
private:
TreeNode<T>* root;
public:
Tree(T data = 0) {
root = new TreeNode<T>(data);
}
// Tree 만들기
/*
A
B C
D E F G
H I J K
*/
void buildTree() {
root->left = new TreeNode<T>('B', new TreeNode<T>('D', new TreeNode<T>('H')),
new TreeNode<T>('E', new TreeNode<T>('I'), new TreeNode<T>('J')));
root->right = new TreeNode<T>('C', new TreeNode<T>('F'),
new TreeNode<T>('G', null, new TreeNode<T>('K')));
}
TreeNode<T>* getRoot() {
return root;
}
void visit(TreeNode<T>* current) {
cout << current->data << " ";
}
// 전위 순회 Current - Left - Right
void preorder(TreeNode<T>* current) {
if (current != null) {
visit(current);
preorder(current->left);
preorder(current->right);
}
}
// 중위 순회 Left - Current - Right
void inorder(TreeNode<T>* current) {
if (current != null) {
inorder(current->left);
visit(current);
inorder(current->right);
}
}
// 후위 순회 Left - Right - Current
void postorder(TreeNode<T>* current) {
if (current != null) {
postorder(current->left);
postorder(current->right);
visit(current);
}
}
};
int main() {
Tree<char> tree('A');
tree.buildTree();
cout << "Preorder >> ";
tree.preorder(tree.getRoot());
cout << endl;
cout << "Inorder >> ";
tree.inorder(tree.getRoot());
cout << endl;
cout << "Postorder >> ";
tree.postorder(tree.getRoot());
cout << endl;
}
4. 테스트

반응형
'알고리듬' 카테고리의 다른 글
| [완전탐색] 문제:소풍(문제 ID: PICNIC, 난이도: 하) (0) | 2021.06.03 |
|---|---|
| [탐욕법] 거스름돈(난이도:하) (0) | 2021.06.02 |
| [DP] LCS(Longest Common Subsequence) 알고리듬 (0) | 2021.05.25 |
| [분할과 정복] 쿼드 트리 뒤집기(문제 ID:QUADTREE, 난이도:하) (0) | 2021.05.24 |
| [분할과 정복] 울타리 잘라내기(문제 ID:FENCE, 난이도:중) (0) | 2021.05.24 |
Comments




