[완전탐색] 문제:소풍(문제 ID: PICNIC, 난이도: 하) 본문
반응형
1. 문제정의
안드로메다 유치원 익스프레스반에서는 다음 주에 율동공원으로 소풍을 갑니다. 원석 선생님은 소풍 때 학생들을 두 명씩 짝을 지어 행동하게 하려고 합니다. 그런데 서로 친구가 아닌 학생들끼리 짝을 지어 주면 서로 싸우거나 같이 돌아다니지 않기 때문에, 항상 서로 친구인 학생들끼리만 짝을 지어 줘야 합니다.
각 학생들의 쌍에 대해 이들이 서로 친구인지 여부가 주어질 때, 학생들을 짝지어줄 수 있는 방법의 수를 계산하는 프로그램을 작성하세요. 짝이 되는 학생들이 일부만 다르더라도 다른 방법이라고 봅니다. 예를 들어 다음 두 가지 방법은 서로 다른 방법입니다.
- (태연,제시카) (써니,티파니) (효연,유리)
- (태연,제시카) (써니,유리) (효연,티파니)
입력
입력의 첫 줄에는 테스트 케이스의 수 C (C <= 50) 가 주어집니다. 각 테스트 케이스의 첫 줄에는 학생의 수 n (2 <= n <= 10) 과 친구 쌍의 수 m (0 <= m <= n*(n-1)/2) 이 주어집니다. 그 다음 줄에 m 개의 정수 쌍으로 서로 친구인 두 학생의 번호가 주어집니다. 번호는 모두 0 부터 n-1 사이의 정수이고, 같은 쌍은 입력에 두 번 주어지지 않습니다. 학생들의 수는 짝수입니다.
출력
각 테스트 케이스마다 한 줄에 모든 학생을 친구끼리만 짝지어줄 수 있는 방법의 수를 출력합니다.
2. 문제 설계
가장 간단한 방법은 완전 탐색을 이용해 조합을 모두 만들어 보는 것입니다. 재귀 호출을 이용해 코드를 만들어 봅시다.
부분 문제 나누기
하나를 짝 지어 놓은 상태에서 아직 짝을 찾지 못한 학생들의 명단이 주어질 때, 친구끼리 둘씩 짝짓는 경우의 수를 계산하면 된다.
3. 구현
#include<iostream>
#include<cstring>
using namespace std;
int n;
bool areFriends[10][10];
int countPairings(bool taken[10]){
//남은 학생 중에 가장 번호가 빠른 학생 찾음(중복을 피하기 위해서)
int firstFree = -1;
for(int i = 0; i < n; i++){
if(!taken[i]){
firstFree = i;
break;
}
}
//base case : 모든 학생이 짝이 맞쳐짐
if(firstFree == -1) return 1;
int ret = 0;
for(int pairWith = firstFree + 1 ; pairWith < n; pairWith++){
if(!taken[pairWith] && areFriends[firstFree][pairWith]){
taken[firstFree] = taken[pairWith] = true; //하나를 짝 지어 놓은 상태
ret += countPairings(taken); //재귀로 나머지 짝을 찾고 수를 계산(완전탐색)
taken[firstFree] = taken[pairWith] = false; //새로운 짝을 만들기 위해 해제
}
}
return ret;
}
int main(){
int testCase, start=0, pair;
bool taken[10];
cin>>testCase;
while(start<testCase){
//초기화
memset(areFriends, false, sizeof(areFriends));
memset(taken, false, sizeof(taken));
cin>>n>>pair;
for(int i=0; i<pair; i++){
int s1,s2;
cin>>s1>>s2;
areFriends[s1][s2] = true;
areFriends[s2][s1] = true;
}
cout<<"OUTPUT : "<<countPairings(taken)<<endl;
start++;
}
return 0;
}4. 테스트
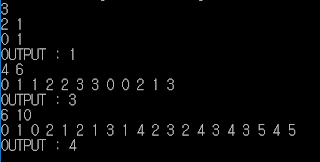
반응형
'알고리듬' 카테고리의 다른 글
| [완전탐색] 시계 맞추기(문제 ID:CLOCKSYNC, 난이도:중) (0) | 2021.06.04 |
|---|---|
| [완전탐색] 게임판 덮기(문제 ID:BOARDCOVER, 난이도:하) (0) | 2021.06.04 |
| [탐욕법] 거스름돈(난이도:하) (0) | 2021.06.02 |
| [트리] 트리(Tree) 순회 (0) | 2021.06.01 |
| [DP] LCS(Longest Common Subsequence) 알고리듬 (0) | 2021.05.25 |
Comments




